A PHYSICIST AT GE RESEARCH LABORATORIES in the 1920s, Frank Benford found that numbers with low first digits occurred more frequently in the world and calculated the expected frequencies of the digits in tabulated data. When Benford tested the first digits in lists of numbers during the 1920s and 1930s, he found that about 31% of the numbers had 1 as the first digit, 19% had 2 , and only 5% had 9.
Benford's Law states that "1" will appear approximately 30 percent of the time as the leading digit whereas "9" will be the leading digit only 4.6 percent of the time. Counterintuitively — you'd tend to think that all single digits would have an equal shot to appear in the first slot — the law holds that the number 9 has the least chance (4.6 percent) to appear in the first slot. Keeping this dictum in mind can be a great help in spotting anomalies in check numbers and payroll statements.
Companies have been using this technique amongst many others in data mining software in fraud investigations!
Two Examples (One from Wikipedia and the other from MARK J. NIGRINI’s whitepaper)
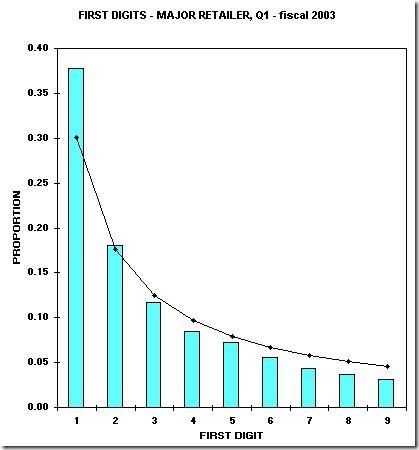
Accounts Payable Numbers : Purchases for resale and other Accounts Payable numbers for a major US retailer for the first fiscal quarter for year-end 2003. This was a large data set with a total dollar value of about $10 billion. Note the good fit to Benford's Law.
First Digit graph
Heights of Tallest Buildings
At tallest structure by category is a table of heights of the 60 tallest buildings in the world. Visual inspection of this table shows that 1 is the most common leading digit. The leading digits of the heights in meters are distributed according to Benford's law!
Sources :
http://en.wikipedia.org/wiki/Benford's_law
http://www.nigrini.com/Benford's_law.htm
http://www.cfo.com/article.cfm/10600143